Akademiets forside | Opgaver til lektion 11 | Lektion 12
Backgammon Akademiet
Lektion 11:
Teknik – at tælle pips
Vi skal vide, om vi er foran eller bagud i ræset. Pipcounten har stor betydning for, hvilket træk der er det bedste i en given position. Derfor er vi nødt til at lære at tælle pips. Det lyder let, men for mange kan det være tidsrøvende og krævende. Bare det at huske sin egen pipcount, mens man tæller modstanderens, kan være en udfordring. I denne lektion vil vi se på genveje og teknikker, som kan gøre optællingen lettere.
Nogle dygtige spillere har altid styr på pipcounten. De tæller fra første rul og laver løbende pipcount, så de aldrig er i tvivl. Det er uden tvivl nyttigt, men kræver meget træning og fuld koncentration under et parti. Vi kan sagtens klare os med mindre.
Det er langt fra altid, at vi har brug for at kende den præcise pipcount. Ofte er det nok at have styr på forskellen mellem spillernes pipcount. Andre gange er det nok blot at vide, hvem der er foran. Vi kan bruge forskellige tællemetoder, afhængigt af situationen. Lad os se på dem.
Når vi skal kende pipcounten præcist
Det kan ske, at brikkerne står "hulter til bulter" på brættet, når vi skal have styr på pipcounten. Og så er ikke andet at gøre, end at tælle pips fra bunden.
Figur 1
I figur 1 er vist en stilling, hvor hvid har brug for at kende pipcounten. Her er der ikke andet at gøre end at tælle fra bunden:
1 brik på 24-punktet plus en brik på 18-punktet giver 42. Plus 3 brikker på 13-punktet giver 39 + 42 = 81. Plus 2 brikker på 12-punktet giver 24 + 81 = 105. Plus 3 brikker på 8-punktet giver 24 + 105 = 129. Plus 3 brikker på 6-punktet giver 18 + 129 = 147. Plus 2 brikker på 4-punktet giver 8 + 147 = 155.
Fik du den? Det kan let gå galt, og langt de fleste vil fare vild i regnestykket, inden optællingen er slut. Men heldigvis er det ofte først senere i et parti, hvor brikkerne er kommet længere frem på brættet, at vi har brug for at kende pipcounten præcist. Og her er der ofte nogle smutveje til at nå det rigtig resultat.
Klyngeoptælling (cluster counting)
Ofte står brikkerne placeret i klynger. Det kan vi benytte os af.
Figur 2
I figur 2 kan vi tælle sorts pips: 3 på 6-punktet giver 18. 4 på 5-punktet giver 20 + 18 = 38. 3 på 4-punktet giver 12 + 38 = 50. De fleste vil formentlig komme frem til det rigtige resultat. Men vi kan faktisk nøjes med at konstatere, at sort har 10 brikker placeret symmetrisk omkring 5-punktet. Mentalt kan vi omarrangere brikkerne: Flyt 3 brikker frem og 3 brikker tilbage, og vi får positionen i figur 3:
Figur 3
10 brikker på 5-punktet giver 50 pips.
Det samme kan vi gøre med hvids position. Vi flytter brikkerne mentalt og konstaterer, at de 10 brikker omkring 8-punktet giver 80 pips. Dvs. at vi med et hurtigt blik på positionen kan tælle både 10 hvide og 10 sorte brikker ret nemt. Det er en enkel manøvre, som ikke kræver megen øvelse. Samtidig vænner vi os til at betragte positionen som en helhed – hvilket vi får god brug for senere.
Figur 4
Med lidt øvelse kan vi bruge metoden til også at optælle klynger, der ikke er helt symmetriske. I figur 4 har sort 10 brikker klumpet sammen omkring 5-punktet, altså i alt cirka 50 pips. Men da én sort brik står 1 pip længere fremme, vi skal trække 1 fra. Sorts pipcount er 49.
Hvid har igen 10 brikker klumpet sammen omkring 8-punktet, i alt cirka 80 pips. Men én hvid brik er 3 pips tilbage, så vi skal lægge 3 til. Hvids pipcount er 83. At få øje på (næsten) symmetriske klynger er en præcis og hurtig metode til optællingen.
Figur 5
En klynge, vi støder på igen og igen, er strukturer, hvor der er brikker på 7- og 8-punkterne. Mentalt kan vi tage udgangspunkt i, at brikkerne er klumpet sammen om "7½"-punktet, men det er bøvlet at holde rede på. I stedet skal vi huske, at 7 + 8 giver 15. I figur 5 har sort 3 par på 7/8-punktet, så sorts pipcount er altså 45. Det samme gælder for hvid, der blot har en brik flyttet en enkelt pip baglæns, så vi skal lægge 1 pip til. Hvids pipcount er 46.
I begyndelsen kan det være svært at se brikkerne som klynger i stedet for som en masse individuelle brikker, men efter noget øvelse bliver det ret naturligt. Når man begynder at kunne se klyngerne, bliver pipcount noget nemmere.
25-reglen
Når klyngerne er talt, er der ofte stadig brikker tilbage, som skal tælles op på anden vis. De fleste gange er vi nødt til at tælle på ”gammeldags” måde, men af og til kan vi benytte os af, at pip-summen for 2 brikker, der står over for hinanden på brættet altid er 25.
Figur 6
Står en brik på 24-punktet, vil den modstående brik stå på 1-punktet, så summen er 25. Står der 2 brikker på 19-punktet og 2 brikker på 6-punktet, vil pip-summen være 2 x 25 = 50. Bruger vi den metode, kan vi hurtigt se, at hvids pipcount i figur 6 er 150.
En par nyttige referencepositioner
Figur 7
I figur 7 har sort 57 pips. De står på den måde, som vi i mange situationer vil stræbe efter, når vi bringer brikker ind, nemlig med mange brikker placeret på 4-, 5- og 6-punkterne. Teoretisk set er det ikke den mest optimale struktur, når der ikke er kontakt, men positionen er let genkendelig og en, vi ofte ser.
Hvis vi kan huske, at referencepositionen (sorts brikker) har 57 pips, er det ganske let at tælle hvids pips. Mentalt kan vi se, at de 2 brikker på 7-punktet er "flyttet" fra 1-punktet. Dvs at hvid har 12 yderligere pips. Hvids pipcount er derfor 69.
Er man komfortabel ved at huske referencepositioner, kan følgende positioner være nyttige at huske:
Figur 8
10 brikker symmetrisk omkring 6-punktet giver 60 pips.
Figur 9
Et lukket bord uden overskydende brikker giver 42 pips.
Figur 10
10 brikker symmetrisk omkring 7-punktet giver 70 pips.
At huske pipcount
Og så er det lige det med at huske tallene. [Hvor ofte sker der ikke det, at vi møjsommeligt har optalt først vores egne pips og derefter modstanderens, blot for at opdage, at vi har glemt vores egen pipcount og må begynde forfra? Det ville være nemt, hvis vi måtte skrive tallene ned, men turneringsreglerne siger klart, at ”det er ikke tilladt for spillerne at bruge elektroniske, mekaniske, skriftlige eller andre hjælpemidler under kampen bortset fra dem, der er nødvendige for at følge stillingen”. Dette tolkes sådan, at det ikke er tilladt at notere pipcount. Så vi må huske.
Selvom vi kun har 10 fingre, kan vi godt bruge fingrene til at huske tal, der er større end 10. Det er faktisk forbløffende enkelt. Vi kan simpelthen benytte ”tegnsprogstallene”. Hvis vi med venstre hånd kan huske ”10'erne” og med højre hånd huske ”1’erne”, kan vi markere resultatet af en optælling med fingrene og er ikke afhængig af hukommelsen. Det kan vi gøre diskret under bordet, så vores modstander ikke kan følge med!
Med tegnsprogstallene kan vi på én hånd ”huske” 9 tal, og det er nok. Tegnene ser således ud:
Figur 11
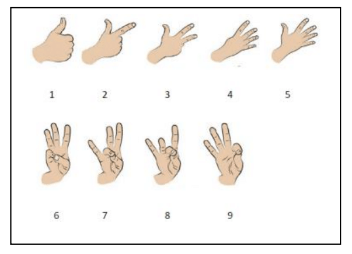
Tallene fra 1 til 5 giver næsten sig selv, mens man lige skal vænne sig til de næste: Tallet 6 får vi ved at berøre lillefingeren med tommelfingeren, tallet 7 ved at berøre ringfingeren med tommelfingeren osv. Tallet 78 ”husker” vi ved på venstre hånd at lave tegnet for 7 (tommelfinger mod ringfinger) og ved på højre hånd at lave tegnet for 8 (tommelfinger mod langfinger). Hvad så, hvis vi skal huske et tal, der er større end 100? Så må vi "glemme" de første 100 og nøjes med at markere de 2 sidste cifre på fingrene og bagefter huske at lægge 100 til.
Når det er nok at kende forskellen
Ofte er det nok at kende forskellen på sin egen og modstanderens pipcount. Det kan vi selvfølgelig finde ud af ved at tælle pips på begge sider og regne forskellen ud. Det er fint, hvis man er skrap til at tælle og hovedregne. Men er man ikke det, kan man i stedet have glæde af mentalt at omarrangere brikkerne på brættet.
Figur 12
I figur 12 starter vi med den hvide brik fra 8-punktet, som mentalt flyttes ind på 2-punktet. Det er 6 pips. Derefter flytter vi den ene af de 2 hvide brikker fra 7-punktet ind på 5-punktet. Det er 2 pips. Hvid er bagud med 8 pips.
Figur 13
I figur 13 har hvid og sort placeret en del brikker symmetrisk over for hinanden. Dem kan vi se bort fra. Flytter vi 2 hvide brikker frem fra 9-punktet til 7-punktet (i alt 4 pips) og en brik tilbage fra 3-punktet til 7-punktet (i alt minus 4 pips) er det let at se, at sorts og hvids pipcount er identisk.
Med lidt øvelse er metoden uhyre effektiv. Skal vi kende pipcounten præcist kan vi starte med at tælle forskellen. Dernæst behøver vi kun at tælle den ene side bagefter for at få pipcounten.
Når vi bare skal vide, hvem der fører
Af og til er det nok at kaste et enkelt blik på brættet for at finde ud af, hvem der fører.
Figur 14
I figur 14 kræver det ikke meget øvelse at se, at sort er foran. Sort står bedre både i sit indre hjemland og i sit ydre hjemland. Vi kan se, at hvis de sorte brikker skal stå på samme måde som de hvide, så skal de alle flyttes baglæns. Så sort fører i ræset.
Figur 15
I figur 15 er det noget sværere at se, hvem der fører. Men det gør sort. Vi kan i princippet se det ved at konstatere, at skal sorts brikker stå som hvids, så skal de alle rykkes baglæns. Men det er bare ikke helt nemt at få øje på. Heldigvis er der også her et par genveje, som dog kræver lidt øvelse.
At tælle crossovers
Ført og fremmest kan man i stedet for at tælle pips tælle crossovers. Men hvad er en crossover? Vi kan betragte brættet som opdelt i 4 kvadranter: Hvids indre hjemland er 1. kvadrant, hvids ydre hjemland er 2. kvadrant, sorts ydre hjemland er 3. kvadrant, og sorts indre hjemland er 4. kvadrant.
At flytte en brik fra én kvadrant til en anden kaldes en crossover. Normalt er det noget, vi har fokus på, når vi prøver at få alle brikker hjem for at undgå en truende gammon, men vi kan også bruge det for at få overblik over ræset.
Alle brikker, der er placeret i 1. kvadrant, skal bruge én crossover for at blive taget af. Brikkerne i 2. kvadrant skal bruge 2 crossovers for at blive taget af. Og så videre.
I figur 15 har hvid 2 brikker i 4. kvadrant. Det er 8 crossovers. Hvid har 3 brikker i 3. kvadrant. Det giver 9 + 8 = 17 crossovers. De 6 brikker i 2. kvadrant giver 12 + 17 = 29 crossovers. Og endelig giver de 4 brikker i eget hjemland 4 + 29 = 33 crossovers. Hvid har 33 crossovers.
På samme måde kan vi tælle de sorte crossovers og komme frem til, at sort har 15 + 10 + 5 = 30 crossovers. I langt de fleste situationer er det spilleren med færrest crossovers, som har færrest pips. Metoden er i familie med den simple optælling, men kræver lidt mindre hovedregning.
Farveløs pipcount
Teknikken bag farveløs pipcount er først og fremmest – som navnet antyder – at man skal prøve at gøre sig farveblind! Princippet er, at man altid kan tage en vilkårlig sort brik og lade den bytte plads med en vilkårlig hvid brik uden at ændre den relative pipcount. Det ændrer selvfølgelig på den absolutte pipcount, men det er vi ligeglade med. Det er forskellen, vi interesserer os for.
Lad os se et eksempel:
Figur 16
I figur 16 vil vi gerne vide, om det er sort eller hvid, der fører ræset. VI kan tælle op, at sort har 25 pips og hvid har 23 pips. Hvid fører altså med 2 pips. Men ideen er jo, at vi gerne vil slippe for at tælle pips. Så hvad gør vi så? Vi bruger farveløs pipcount!
Mentalt flytter vi de hvide brikker over på vores egen side af brættet. Det gør vi ved at lade den sorte brik på 3-punktet bytte plads med den hvide brik på 21-punktet. Nu "ser" det sådan ud:
Figur 17
Nu har pipcounten selvføgelig ændret sig. Men forskellen er den samme. Hvid fører med 2 pips – altså samme resultat som før. Men det er meget lettere at se i figur 17 end i figur 16.
I figur 16, hvor begge spillere har 2 brikker tilbage på brættet, sammenligner vi simpelthen de to brikker, der står tættest på vores egen udtagning, med de to brikker, der står tættest på modstanderens udtagning.
Lad os se et andet eksempel:
Figur 18
Vi kan tælle op på den traditionelle måde og komme frem til, at hvid og sort begge har 29 pips. Men vi kan også bare kaste et blik på strukturene på begge sider af brættet. De er ens. På begge sider af brættet står der én brik på 4-punktet, to brikker på 3-punktet og én brik på 2-punktet. Men så er pipcounten også ens! Tag den hvide brik på 21-punktet og byt med den sorte brik på 4-punktet, så er det indlysende. Strukturerne er ens. Derfor er pipcounten også ens.
Når vi benytter farveløs pipcount, ser vi bort fra brikkernes farve og fokuserer i stedet på struktur.
Normalt vil vi reservere brugen af farveløs pipcount til de situationer, hvor begge spillere har alle brikker på brættet, hvor der er meget kontakt, og hvor positionen er asymmetrisk. De situationer optræder hele tiden, og meget ofte har vi i de positioner brug for at vide, hvem der er foran. Samtidig er det besværligt at tælle traditionelt, så i stedet for at gætte os frem, kan vi bruge den farveløse pipcount.
Så lad os lige kaste et blik på stillingen fra figur 15 én gang til:
Figur 19
Hvem fører ræset? Det gør sort. Umiddelbart kan det være svært at afgøre uden at tælle, men i figur 15 konstaterede i. at skal sorts brikker stå som hvids, så skal de alle rykkes baglæns. Så sort må føre. Men vi kan også prøve at sammenligne strukturerne.
Vi tæller op og kikker på de 15 brikker, der står nærmest på 1-punktet. Tilfældigvis står der 15 brikker på den hvide side af brættet, som vi så skal sammenligne med de 15 brikker på den sorte side af brættet. Gør vi det, kan vi nærmest med et enkelt blik afgøre, at hvid er bagud i ræset. Faktisk har vi allerede gjort det én gang i figur 14!
Lad os lige se på stillingen igen:
Figur 20
Det er let at se, at hvid er bagud i ræset. Det er måske lidt mindre let at se, at strukturerne i figur 19 og 20 er nøjagtig ens, men det er ikke desto mindre tilfældet. Ved farveløs pipcount er princippet, at når vi fx betragter figur 19, så skal vi se bort fra farverne og i stedet for vores indre øje se figur 20.
Måske virker metoden bedst for de visuelt anlagte, men så snart man har accepteret, at metoden er korrekt, er det blot et tilvænningspørgsmål. Er forskellen større end 10 pips, kan metoden være hurtigere end en optællings- og hovedregningsmetode. Kunsten er at gøre sig farveblind!
Opsummering
For at vide, hvem der fører i ræset, skal vi kunne tælle. Tællemetoden afhænger af, om vi skal vide, hvem der er foran, hvor stor føringen er, eller hvad den præcise pipcount er. I alle tilfælde er der metoder, som med lidt øvelse kan gøre livet lettere og optællingen mere præcis.
læs mere
- Paul Magriel: "Backgammon", kap1: Rules